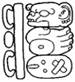
·    Glyph-C forms one of the standard components of the SS.

·    It consists of one of these 3 godheads, surrounded by other elements:

o (Optional) u: QRG Stela A A8, QRG Stela E C7, QRG Stela F C7 in the examples above.

o A number between 1 and 6.

o One of the 3 god-heads.

o A right hand with fingers outstretched (K’AL).

o The right-side reduced variant of the “moon glyph” – ja.

o (Optional) li: QRG Stela E B6b, QRG Stela E C7, QRG Stela J B13 in the examples above.

·    ScheleEtAl-TLSiCMI.p4:

o First realization that there are 3 heads, and that they follow one another in a cyclical pattern, with coefficients of 1, 2, 3, 4, 5, 6 for each head, before moving on to the next head.

o Recognition that the JGU-head (CHUWAJ) may be replaced by just the eye of the JGU (with the cruller underneath) – e.g., QRG Stela I B5 in the examples above.

·    The general format is: <optional-u-or-ta>-<lunation-#>-<god-head>-K’AL-ja.

·    There is some freedom in the placing of the lunation-#, god-head, K’AL, and ja. Specifically:

o The lunation-number is usually vertically long, along the left side, but can also horizontally long, along the top.

o K’AL is generally at the bottom centre, the freedom lies between:

§ <<god-head>.ja>:K’AL (more common), or

§ <<god-head>:K’AL>.ja (less common)

o Is there a possibility that the K’AL and ja might be a HUL, despite the placement being slightly different from the more common HUL which has the index finger actually pointing to / touching the top part of the moon (while the K’AL hand in Glyph-C doesn’t point at all, and the index finger is either not at all in contact with the moon (<<god-head>.ja>:K’AL), or if it is, then not with the top part of the moon (<<god-head>:K’AL>.ja))? Dorota Bojkowska: open question, don’t exclude this possibility (but not that likely). Also, Albert Davletshin & Dimitri Beliaev have a theory about K’AL being a “room” (as a noun) rather than a verb (see below).

·    The three god-head glyphs are:

o DG = Death God (Kimi, see Bratislava workbook, with Guido Krempel & John Chuchiak on codices and gods).

o TMG = Tonsured Maize God (Ixiim).

o JGU = Jaguar God of the Underworld (Chuwaj):

§ Note that in the slide shown in AT-YT2021-lecture21.t0:06:23, Chuwaj is transcribed with a long-a: Chuwaaj.

The subscript numbers in Glyph-C_n with n=1, 2, 3 have no particular significance. They occur cyclically, so it is purely arbitrary which one is considered 1 (though the cyclic order is of course fixed).

·    The exact reading of Glyph-C – with all the other elements – is not completely certain, but should include the words of the god-head: Kimi, Ixiim, Chuwaj.

·    Sergei Vepretskii & Dmitri Beliaev’s idea: in Glyph-C, K’AL isn’t a verb, it’s a noun:

o This is known in Yucatec, and means “room”.

o A room in the sky, and there were 6 such rooms, and every month the deity in question goes to that specific room.

o “This and this day, the TMG arrived to the x-th room”.

o There are probably no existing papers, as this is a new theory.

·    The time it takes to go from new moon to new moon, or from full moon to full moon) is approximately 29.5 days, and 6 x 29.5 = 177. Each (calendar) lunation is made to have a whole number of days. This is often said to be because Maya mathematics “doesn’t have fractions”, but it’s actually because having fractions wouldn’t help anyway: one still needs to have a whole number of days in a lunation. For example, Western mathematics does have fractions, but the 1/4 day of the 365 + 1/4 days of the time it takes for the earth to go around the sun still needs to be dealt with – one still needs to have a whole number of days in a year.

o 29 x 6 = 174 would be 3 days short of 6 real lunations =177 days.

o 30 x 6 = 180 would be 3 days in excess of 6 real lunations = 177 days.

o So the ideal solution is to have 3 lunations of 29 days and 3 lunations of 30 days, e.g. 29, 30, 29, 30, 29, 30 = 177 days.

§ One could consider the 30th day of every other lunation to be the extra day, to adjust for the shortfall of the nominal 29 days in a lunation. This is almost as if every other lunation was a "leap month", in the same way as every fourth year in the Western calendar is a "leap year", to adjust for the shortfall of the nominal 365 days in a year.

§ There are hence 6 such lunations per 177-day period = "lunar half year":

·      Calling it a “lunar half year” makes sense, as 177 x 2 = 354, which is slightly less than the number of days in a year.

·      Alternatively, each lunation is a month, so six lunations is a "lunar half year", half of twelve lunar months.

·      The term "lunar half year" comes from Yesugi&Saito-GYotMSS.p2 (1991) but isn’t used that often (given here just for the sake of completeness).

·    Glyph-C hence gives both which of the three "lunar half years" (JGU, DG, or TMG), as well as which of the 6 lunations of that “lunar half year” it is, i.e. where the date of the LC of the event indicated by the ISIG falls, in this cycle of 18 (= 6 x 3) lunar half years. Glyph-A, in turn, indicates whether that lunation (i.e. the lunation of the day which the LC of the event indicated by the ISIG) has 29 or 30 days (see also Glyph-A).

·    More examples are given under each of the separate Glyph-C_n, for n=1, 2, 3.